ΠΑΡΟΣ: Η βιωματική πειραματική μάθηση: Το πείραμα του Ερατοσθένη πραγματοποίησαν μαθητές του Γυμνασίου Πάρου - με την εποπτεία καθηγητών τους

Μαθητές του Γυμνασίου Πάρου συμμετείχαν στην πραγματοποίηση του πειράματος του Ερατοσθένη που διοργανώθηκε από τα ΕΚΦΕ Σερρών, Κατερίνης, Σπάρτης, Μυτιλήνης και 1^ο Ηρακλείου. Με το πείραμα αυτό οι μαθητές του Β4 μαζί με τους εκπαιδευτικούς Βασάλου Δήμητρα, Μηλαίου Μαρούλα  Κεφάλα Φραγκίσκο μέτρησαν την ακτίνα της Γης. Το αποτέλεσμα της μέτρησης των μαθητών του Γυμνασίου μας ήταν 6444,8 Km με σφάλμα μόλις 1,16% σε σχέση με τα 6370 Km που είναι η πραγματική τιμή. 

 

  Περισσότερες λεπτομέρειες για το πείραμα στην σελίδα

20-21/03/2016 Το πείραμα του Ερατοσθένη

  Η Κυριακή 20 Μαρτίου (εαρινή Ισημερία) μπορεί να  χαρακτηριστεί ως η αρχή της Άνοιξης. Τη συγκεκριμένη ημερομηνία ο Ήλιος βρίσκεται ακριβώς πάνω από τον ισημερινό της Γης, με αποτέλεσμα η νύχτα και η μέρα να έχουν ίση διάρκεια σε οποιοδήποτε σημείο της γήινης επιφάνειας. Τη μέρα αυτή είναι μια καλή ευκαιρία να επαναλάβουμε το πείραμα του Ερατοσθένη επειδή γνωρίζουμε τον τόπο που ο Ήλιος ρίχνει τις ακτίνες του κατακόρυφα. Λόγω της κυριακάτικης αργίας η εκτέλεση του πειράματος προτείνεται να γίνει τη Δευτέρα 21 Μαρτίου 2016. Η δράση με τίτλο: «Το Πείραμα του Ερατοσθένη για τον υπολογισμό της ακτίνας της Γης» διοργανώνεται από τα ΕΚΦΕ Σερρών, Κατερίνης, Σπάρτης, Μυτιλήνης και 1^ο Ηρακλείου, με την υποστήριξη της ΠΑΝΕΚΦΕ. Στη δράση μπορούν να συμμετέχουν ομάδες μαθητών, με την καθοδήγηση των εκπαιδευτικών τους από όλα τα σχολεία της χώρας. Το πείραμα αυτό έχει χαρακτηριστεί ως ένα από τα 10 πιο όμορφα πειράματα στην ιστορία της φυσικής.

Λίγα λόγια για την ιστορία του πειράματος

 Ο Ερατοσθένης (3ος π.Χ. αιώνας) ήταν Διευθυντής της μεγάλης Βιβλιοθήκης της Αλεξάνδρειας, όπου σε έναν πάπυρο διάβασε ότι το μεσημέρι της 21ης Ιουνίου (θερινό ηλιοστάσιο), στα νότια όρια της πόλης Συήνη (Ασσουάν), οι κατακόρυφοι στύλοι δεν ρίχνουν καθόλου σκιά και ο Ήλιος καθρεφτίζεται ακριβώς στον πυθμένα ενός πηγαδιού (δηλαδή, βρίσκεται στο Ζενίθ του τόπου). Ως επιστήμονας, λοιπόν, ο Ερατοσθένης διερωτήθηκε, εάν συμβαίνει το ίδιο ταυτόχρονα και σε μια άλλη πόλη πχ. στην Αλεξάνδρεια. Όμως στην Αλεξάνδρεια, κατά την ίδια μέρα και ώρα, οι κατακόρυφοι στύλοι έριχναν σκιά.Αν η Γη ήταν επίπεδη, οι κατακόρυφοι στύλοι στις δυο πόλεις θα ήταν παράλληλοι και θα έπρεπε και οι δυο να ρίχνουν σκιά. Αφού, λοιπόν, αυτό δεν είναι αλήθεια, τι μπορεί να συμβαίνει; Την απάντηση έδωσε ο Ερατοσθένης υποστηρίζοντας ότι η επιφάνεια της Γης δεν είναι επίπεδη αλλά σφαιρική. Αυτό το συμπέρασμα είναι, προφανώς, θεμελιώδους σημασίας και επιπλέον επέτρεψε στον Ερατοσθένη να προσδιορίσει την ακτίνα και το μήκος της περιφέρειάς της Γης. Πραγματικά, από το μήκος της σκιάς υπολογίζεται αμέσως η διαφορά των γεωγραφικών πλατών των δύο πόλεων, ίση περίπου με 7 μοίρες. Επειδή η απόσταση των δύο πόλεων ήταν γνωστή από αφηγήσεις βηματιστών και ίση περίπου με 800 Km (φημολογείται ότι ο Ερατοσθένης μίσθωσε βηματιστές για τη μέτρησή της), η περιφέρεια της Γης υπολογίστηκε ίση με 40000 Km.Αυτή είναι η σωστή απάντηση και ο Ερατοσθένης την έδωσε χρησιμοποιώντας ως μόνα εργαλεία ράβδους, μάτια, πόδια, μυαλό με απλότητα σκέψης και επινοητικότητα. Το λάθος στον υπολογισμό ήταν μόνο 2%, ένα πραγματικά αξιοσημείωτο επίτευγμα για περίπου πριν από 2,5 χιλιετίες. Άρα, ο Ερατοσθένης ήταν ο πρώτος άνθρωπος που μέτρησε τις διαστάσεις του πλανήτη Γη, γι' αυτό και θεωρείται δημιουργός της μαθηματικής γεωγραφίας.

Οδηγίες για την εκτέλεση του πειράματος

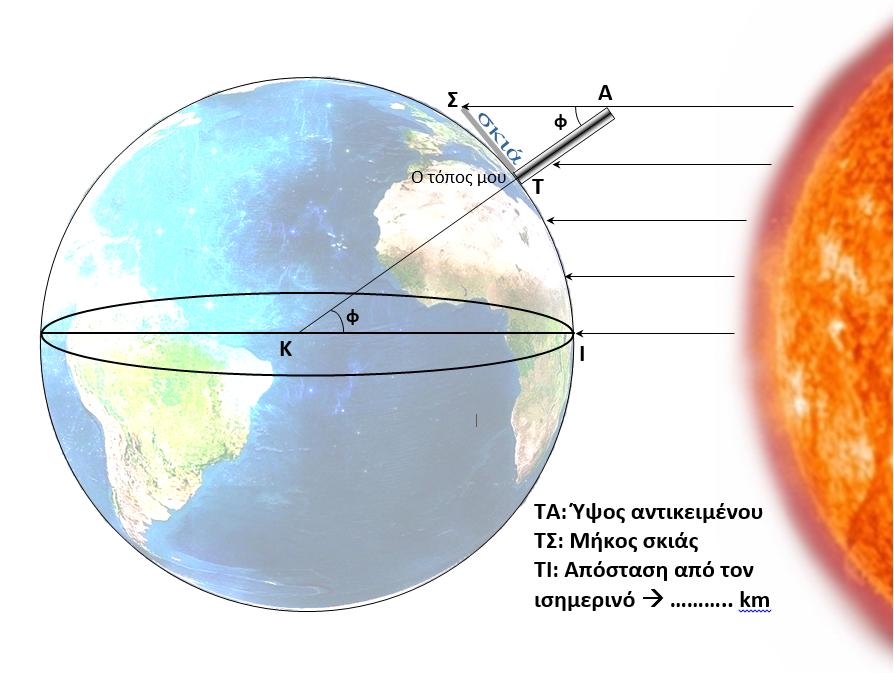
  Αν θεωρήσουμε ότι ο κύκλος στο διπλανό σχήμα είναι η Γη τότε η έλλειψη στο κέντρο είναι ο ισημερινός. Στον ισημερινό αυτές τις μέρες ο Ήλιος το μεσημέρι βρίσκεται στο ζενίθ. Επομένως οι ακτίνες πέφτουν κατακόρυφα και ο Ήλιος καθρεφτίζεται στον πυθμένα ενός πηγαδιού. Η προέκταση μιας ακτίνας του είναι η ΙΚ και περνάει από το κέντρο της Γης Κ.
Έστω ότι εμείς είμαστε στη θέση Τ. Αν τοποθετήσουμε μια κατακόρυφη ράβδο ΤΑ=Υcm τότε αυτή το μεσημέρι (στις 12:34 μ.μ. για τις Σέρρες) έχει σκιά ΤΣ=Χcm.
Σημ. Βρείτε εδώ την ώρα που πρέπει να κάνετε τη μέτρηση σε κάθε τόπο
Υπολογίζουμε την εφαπτομένη της γωνίας ΣΑΤ από το λόγο Χ/Y και έτσι βρίσκουμε την γωνία που είναι φ μοίρες. Η γωνία φ είναι ίση με την επίκεντρη γωνία ΤΚΙ. Το γεωγραφικό πλάτος της θέσης μας είναι φ μοίρες.
Παρατήρηση: Η γωνία φ είναι ίση με το γεωγραφικό πλάτος μόνο αν η μέτρηση γίνει τις μέρες της εαρινής ή φθινοπωρινής ισημερίας.Από το google earth ή από εδώ βρίσκουμε την απόσταση ΤΙ=S. Είναι η απόσταση της θέσης μας από τον Ισημερινό. Με μια απλή αναλογία υπολογίζουμε την περίμετρο της Γης και μετά την ακτίνα της R.